最长公共子序列（LCS）与最长公共子串（DP）

1.子串与子序列的区别

这里给出一个例子：有两个母串

cnblogs
belong

比如序列bo, bg, lg在母串cnblogs与belong中都出现过并且出现顺序与母串保持一致，我们将其称为公共子序列。最长公共子序列（Longest Common Subsequence,LCS），顾名思义，是指在所有的子序列中最长的那一个。子串是要求更严格的一种子序列，要求在母串中连续地出现。在上述例子的中，最长公共子序列为blog（cnblogs,belong），最长公共子串为lo（cnblogs, belong）。

2.DP状态转移方程

最长公共子序列（LCS）：

二维数组c[i][j]记录串x1x2⋯xi与y1y2⋯yj的LCS长度，得到转移方程

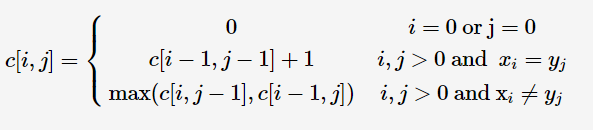
最长公共子序列
核心代码如下：

int lcs(String str1, String str2) {  
    int len1 = str1.length();  
    int len2 = str2.length();  
    int c[][] = new int[len1+1][len2+1];  
    for (int i = 0; i <= len1; i++) {  
        for( int j = 0; j <= len2; j++) {  
            if(i == 0 || j == 0) {  
                c[i][j] = 0;  
            } else if (str1[i-1] == str2[j-1])) {  
                c[i][j] = c[i-1][j-1] + 1;  
            } else {  
                c[i][j] = max(c[i - 1][j], c[i][j - 1]);  
            }  
        }  
    }  
    return c[len1][len2];  
}

算法复杂度等于将所给两个字符串各扫一遍，故为o(m*n)

最长公共子串（DP）：

与子序列的不同仅在于当Xi不等于Yj时，对应的dp记为0
二维数组c[i][j]用来表示以XiYj为结尾的公共子串的长度（注意此处的dp还需要找其中公共子串的最大值），得到转移方程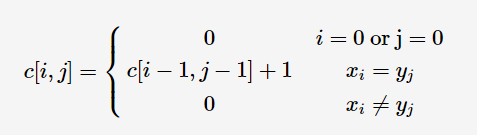
最长公共子串
核心代码如下：

int lcs(String str1, String str2) {  
    int len1 = str1.length();  
    int len2 = str2.length();  
    int result = 0;     //记录最长公共子串长度  
    int c[][] = new int[len1+1][len2+1];  
    for (int i = 0; i <= len1; i++) {  
        for( int j = 0; j <= len2; j++) {  
            if(i == 0 || j == 0) {  
                c[i][j] = 0;  
            } else if (str1[i-1] == str2[j-1])) {  
                c[i][j] = c[i-1][j-1] + 1;
                result = max(c[i][j], result);    
            } else {  
                c[i][j] = 0;  
            }  
        }  
    }  
    return result;  
}

最长回文串问题

可转换为最长子串问题，即将原始序列reverse，再求解该序列和原序列的最长公共子串即可，例题见：PAT 1040

允许重复元素的LCS

试题举例：PAT 1045. Favorite Color Stripe (30)
此题按照正常的思路求解，应该使用最长公共子序列算法LCS，但与常规的LCS有所差别，常规LCS是从两个序列中按索引递增顺序，不重复的选取最大公共子列，而现在的问题是在序列B中按照A中的元素顺序可重复的找出最大子列，这样说起来比较抽象，下面举个例子，对于序列：

A=｛2,3,1,5,6｝ B={2,2,4,1,5,5,6,3,1,1,5,6}

如果是常规的LCS，我们找到的子列将会是{2,3,1,5,6}，因为B完全的包含了A（不必连续）
如果是可重复的LCS，我们完全可以选择{2,2,3,1,1,5,6}，这便是变种的LCS。

本题与LCS相比，唯一的差别在于最长公共子串的字符可以连续出现。故我们在x[i]==y[j]，即串尾匹配时，不应像LCS那样c[i][j]=c[i-1][j-1]+1，因为这样表明串尾字符不能参与前面的匹配了，即同一个字符不能连续进行匹配。应该c[i][j]=max(c[i-1][j],c[i][j-1])+1，x[i]和y[j]依然可以参与前面的匹配。

（这里要不要加和c[i-1][j-1]的比较都可以，从结果看不影响）

核心代码如下：

vector<vector<int> > c(n+1,vector<int>(m+1,0));
	for(int i=1;i<=n;i++){
		for(int j=1;j<=m;j++){
			if(a[i-1]==b[j-1])//串尾相等
				c[i][j]=max(c[i-1][j],c[i][j-1])+1;//对于LCS，此处是c[i][j]=c[i-1][j-1]+1
			else
				c[i][j]=max(c[i-1][j],c[i][j-1]);
		}
	}
	cout<<c[n][m];

最大子段和

给定一个序列为a1,a2,a3……an;

要求：求出这个序列里面找到一个子段和最大

dp[i]表示以第i个元素结束的最大子段和

如果dp[i-1]>0,无论ai为何值，有dp[i]=dp[i-1]+ai;

如果dp[i-1]<=0;舍弃，重新令dp[i]=ai;(因为dp[i-1]为负数无论ai为什么值加上去都会减少)

状态转移方程如下：

dp[i]=dp[i-1]+ai (dp[i-1]>0)

dp[i]=ai(dp[i-1]<=0)

核心代码如下：

dp[0] = a[0];
max = a[0];
for (int i = 1; i<n; i++) {
    if (dp[i-1] > 0) {
        dp[i] = dp[i-1] + a[i];
    }else{
        dp[i] = a[i];
    }
    if (dp[i] > max) {
        max = dp[i];
    }
}
return max;

若需要记录子段的起始位置，则可如下方式记录：

//此处省去了dp[i]数组，改用tmp去记录
//通过lindex记录起始的子段位置，rindex记录终点的子段位置
 while (cin >> n) {
     lindex = tmp = tmpindex = 0;
     max = -1;//注意此处max应为-1；
     rindex = n-1;
     for (int i = 0; i<n; i++) {
         cin >> a[i];
         tmp += a[i];
         if (tmp < 0) {
             tmp = 0;
             tmpindex = i+1;
         }else if (tmp > max) {//注意此处一定要是else if结构
             max = tmp;
             rindex = i;
             lindex = tmpindex;
         }
     }

最长递增子序列（LIS）

给定一个序列，求解它的最长递增子序列的长度。比如： arr[] = {3,1,4,1,5,9,2,6,5} 的最长递增子序列长度为4。即为：1,4,5,9

当 arr[i] > arr[j]，lis[i] = max{lis[j]}+1 ；其中，j 的取值范围为：0,1…i-1

当 arr[i] < arr[j]，lis[i] = max{lis[j]} ；其中，j 的取值范围为：0,1…i-1

dp[i]表示以第i个数字为结尾的最长递增子序列长度，最长递增子序列的递推公式为：

dp[1] = 1;
dp[i] = max{1, F[j] + 1 | aj < ai & & j < i};

核心代码：

def lengthOfLIS(self, nums: List[int]) -> int:
  if not nums: return 0
  dp = [1] * (len(nums) + 1)
  for i in range(len(nums)):
  	for j in range(i)://遍历其前所有数字
  		if nums[i] > nums[j]:
  			dp[i] = max(dp[i], dp[j] + 1)
  ans = 0
  for i in dp: //找到以每一个元素结尾的最长递增子序列中的最大值,该最大值即为答案
  	ans = max(ans, i)
  return ans

若所需最长递减子序列，则同理，只需把求解tmax 的判断条件改写成

 if (list[i] <= list[j]) { 
	 ……
}

参考资料：

https://blog.csdn.net/qq_31881469/article/details/77892324

https://blog.csdn.net/xyt8023y/article/details/46910283

https://blog.csdn.net/sun897949163/article/details/49559679

《王道计算机考研机试指南》